はじめに

はむです．想像以上に小難しい話になってしまいました．
御託はいいからさっさと回路見せろ！！！というせっかちさんはマイクラ世界での論理演算に飛んでください．(｡＞﹏＜)
マイクラなんかどうでもいいから論理回路入門させろ！！！といういけずさんはこちらに．(｡＞﹏＜) 論理回路基礎(UTokyo OpenCourseWare)

論理関数

基本論理回路と真理値表

ブール代数

論理演算は以下の演算規則に従って代数的に考えることができます．※真理値表参照
（交換法則，結合法則，分配法則，和と積の双対性，ド・モルガンの定理が成立します．）

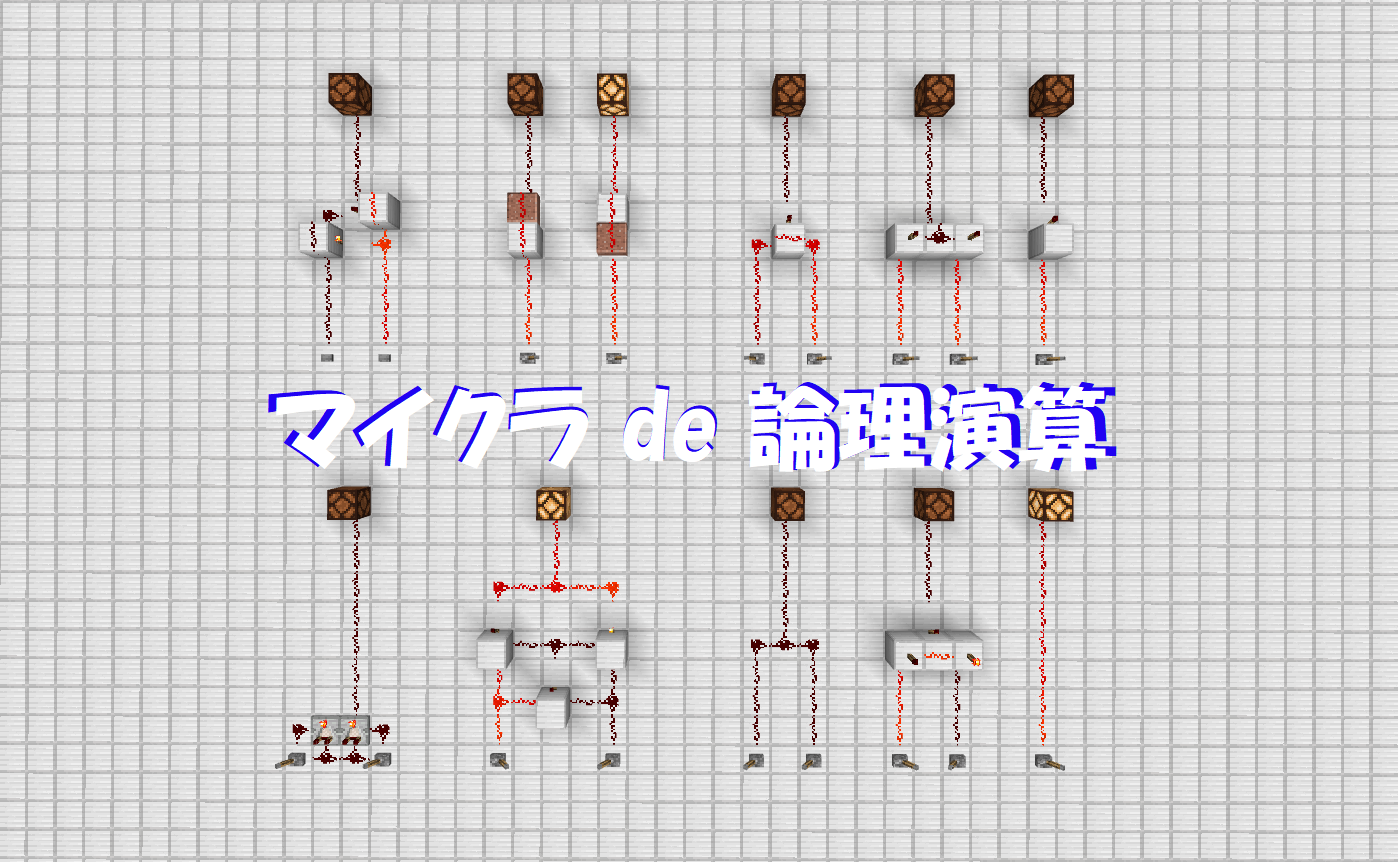
マイクラ世界での論理演算

基本論理回路

マインクラフトではレッドストーン（以下RSと呼称）パウダーとそれを使ったトーチを用いて回路を引きます．
NOTを見て分かる通り，RSトーチは設置されているブロックのRS情報を反転させる働きがあり，これを利用して基本論理回路が組まれます．

AND，NOR，EQUIVはそれぞれ，NAND，OR，XORにNOTを噛ませるとできます．

NANDに関しては，スイッチ2つを1にした時だけ真ん中のブロックにRS信号が伝わらなくなり，出力が0になります．（それ以外の場合は2つあるRSトーチのうちどちらかは反転しないので１を出力します．）

XORは，NOR3つとOR1つからなっています．（詳細は後述） また，RSコンパレータ（比較，減算装置）を組み合わせるとよりコンパクトにできます．（話すと長くなるので詳しくはまた別の機会に．）

基本論理回路以外にも，ダイオード（情報を一通にする）やラッチ回路（1bitの情報を保存できる）などもあります． ご自身でいろいろ試してみてください．
RS回路(基礎)   RS回路(応用)
（ちなみに，マイクラはチューリング完全なのでマイクラでマイクラが作れたりするよ！）

補足説明

標準形について

ex) $X_1⊕X_2=f(X_1, X_2)=X_1⋅\overline{X_2}+\overline{X_1}⋅X_2 -(1)$

加法標準形：論理積の論理和

• 利点：設計が平易で機械的，出力の遅延は3段分
• 欠点：無駄が多い（真理値表の「1」の数だけAND／ORゲートが必要）
  →簡単化が必要

簡単化とは……AND／OR素子の入力数を減らし，回路の総量と遅延時間を短くすること．

特に以下の3式が重要．（和と積の双対性が成立している．）
$X+(X⋅Y)=X, X+(\overline{X}⋅Y)=X+Y, (X⋅Y)+(X⋅\overline{Y})=X$
$X⋅(X+Y)=X, X⋅(\overline{X}+Y)=X⋅Y, (X+Y)⋅(X+\overline{Y})=X$

XOR回路

以下，例としてXOR回路についての簡単化を示す．（前項画像参照）

$Y=\overline{X_1+X_2}$
$Z_1=\overline{X_1+Y}, Z_2=\overline{X_2+Y}$

$XOR(X_1, X_2)$
$=(X_1+X_2)⋅(\overline{X_1⋅X_2}) -(*)$ （ベン図を論理式に起こす．） $=(\overline{X_1}⋅X_2)+(X_1⋅\overline{X_2}) -(1)$ （加法標準形）
$=(X_1+X_2)⋅(\overline{X_1}+\overline{X_2})$    （乗法標準形）
$=(X_1+X_2)+\overline{X_1}+(X_1+X_2)+\overline{X_2}$
$=\overline{(\overline{X_1+X_2})+X_1}+\overline{(\overline{X_1+X_2})+X_2}$
$=\overline{X_1+Y}+\overline{X_2+Y}$
$=Z_1+Z_2$

おわりに

ここまで読んでいただきありがとうございます．
他に何も書くことがなかったので適当にRS回路組んで紹介するか～と書き始めた本記事ですが，論理演算が想像以上に奥が深くてそれだけで一記事書けてしまいました．
某大学のPDFを流し読みして適当に要点をまとめただけなので，どこかおかしいところがあっても責めないであげてください．（そっとDMなんかで教えていただけると嬉しいです．）（感想もくれ）
本当は計算機とか時計とか作って完成形どーーーん！ってする予定だったんですが，分量的にいい頃合いですし〆切ギリギリで時間ないですしおすしまた次回にします．楽しみにしていてください．
最後に，参考にさせていただいた講義のリンクを貼っておきます．論理回路に興味のある方は是非覗いてみてください．
論理回路基礎(UTokyo OpenCourseWare)