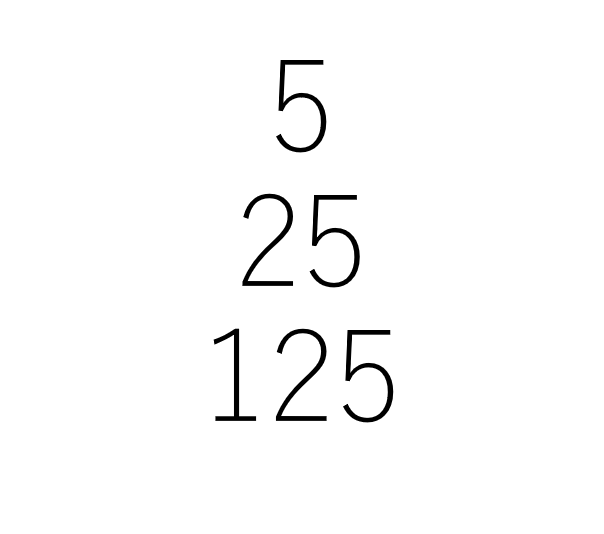$n = 1$ のとき,

5 は 全ての桁の数字が奇数で,

$5^1 (= 5)$ の倍数かつ 1 桁の数です.

$n = 2$ のとき,

75 は 全ての桁の数字が奇数で,

$5^2 (= 25)$ の倍数かつ 2 桁の数です.

$n = 3$ のとき,

375 は 全ての桁の数字が奇数で,

$5^3 (= 125)$ の倍数かつ 3 桁の数です.

問題

任意の自然数 $n$ について, すべての桁の数字が奇数である $n$ 桁の $5^n$ の倍数が存在することを示せ.

証明

数学的帰納法によって示す.

① $n = 1$ のとき

自明である. (5 が題意を満たす)

② $n = l　( l\geqq2, l\in\mathbb{N})　$ で命題が成立すると仮定したとき

$5^l$ の倍数で, 各桁の数字が奇数である $l$ 桁の自然数を

$m = a \times 5^l　(a\in\mathbb{N})　$ とする.

このとき,

$\mathbb{A} = $ {$b \times 10^l + m | b = 1, 3, 5, 7, 9$}

の各要素は各桁の数字が全て奇数である $l+1$ 桁の自然数であるから, これらの中に $5^{l+1}$ の倍数があることを示せばよい.

各要素を $5^l$ で割ると

$\mathbb{A’} = $ {$b \times 2^l + a | b = 1, 3, 5, 7, 9 $}

となる. ここで 5 を法として

$i \times 2^l + a \equiv j \times 2^l + a$

となる自然数 $i, j (i, j \in b, i < j)$ が存在すると仮定すると,

$(j - i) \times 2^l \equiv 0$　・・・(式 1)

となるが, 任意の $l,i, j$ の組について $2^l$ と $(j - i)$ は 5 と互いに素であるから (式 1) は成立し得ない. よって, $\mathbb{A’}$ の各要素はそれぞれ 5 を法として互いに合同ではないので, これらの中に 5 の倍数は 1 つ存在する.

従って, $\mathbb{A}$ の要素の中には 1 つ $5^{l+1}$ の倍数が存在する.

①, ②より数学的帰納法から題意は示された.

追加問題

任意の正の奇数について, 各桁の数字が全て奇数である倍数が存在することを示せ.

証明

① 5 の倍数以外の奇数について

5 の倍数以外の奇数からなる集合を $\mathbb{K}$ とする. また自然数 $n$ を $m$ 回繰り返した数を $Rep(n, m)$ と定義する. 例えば

$Rep(33, 4) = 33333333$

である. ここで $\forall k \in \mathbb{K}$ について,

$\mathbb{M} = $ {$Rep(1, t) | t = 1, 2, 3, … , k + 1$}

を考える. 鳩ノ巣原理より, $\mathbb{M}$ の要素の中には $k$ を法として合同な組が少なくとも 1 つ存在するので, これらを $i, j \in t, i < j$ として

$Rep(1, i), Rep(1, j)$

とする. このとき,

$Rep(1, j) - Rep(1, i) = Rep(1, j - i) \times 10^i$

となり, これは $k$ の倍数でないといけない. $k$ と $10^i$ は互いに素であるから, $Rep(1, j - i)$ は $k$ の倍数であり, 各桁の数字が全て奇数である.

② 5 の倍数の奇数について

5 の倍数の奇数からなる集合を

$\mathbb{F} = $ {$b \times 5^l | b \in \mathbb{K}, l \in \mathbb{N}$}

とする. ここで $\forall f = b \times 5^l \in \mathbb{F}$ について先ほどの問題より,
すべての桁の数字が奇数である $l$ 桁の $5^l$ の倍数が存在するので, これを $x$ とする. そして,

$\mathbb{X} = $ {$Rep(x, t) | t = 1, 2, 3, … , b + 1$}

を考える. 鳩ノ巣原理より, $\mathbb{X}$ の要素の中には $b$ を法として合同な組が少なくとも 1 つ存在するので, これらを $i, j \in t, i < j$ として

$Rep(x, i), Rep(x, j)$

とする. このとき,

$Rep(x, j) - Rep(x, i) = Rep(x, j - i) \times 10^{li}$

となり, これは $b$ の倍数でないといけない. $b$ と $10^{li}$ は互いに素であるから, $Rep(x, j - i)$ は $b$ の倍数であり, また $b$ と $5^{l}$ も互いに素であることから, $Rep(x, j - i)$ は $f$ の倍数であり, 各桁の数字が全て奇数である.

よって①, ②より題意は示された.

あとがき

解けましたでしょうか ? これは, 高 3 の頃にふと思いついた問題で案外簡潔に証明できたと思っていたものでした. 正直, あっている自信は無いのでもしより良い証明方法があったり, そもそも命題が成り立たないよって分かった方は是非ご連絡ください. 場合によっては土下座しないといけません. よろしくおねがいします.

競プロって結構整数問題を含んでいて, つらいなぁと感じます…